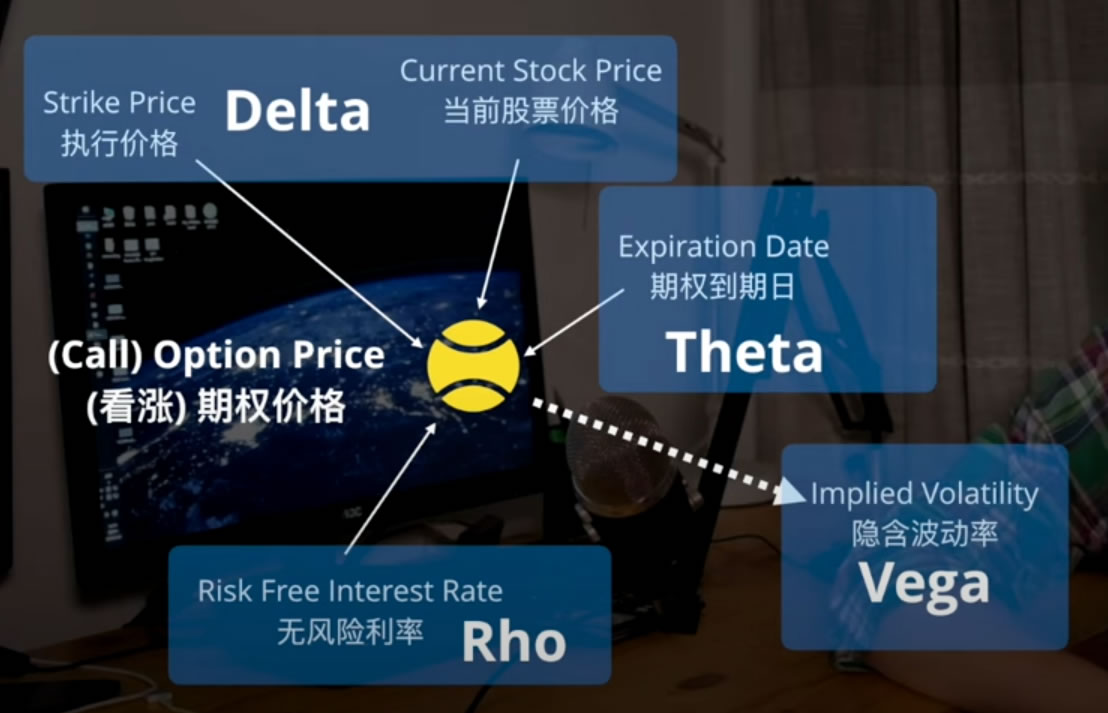
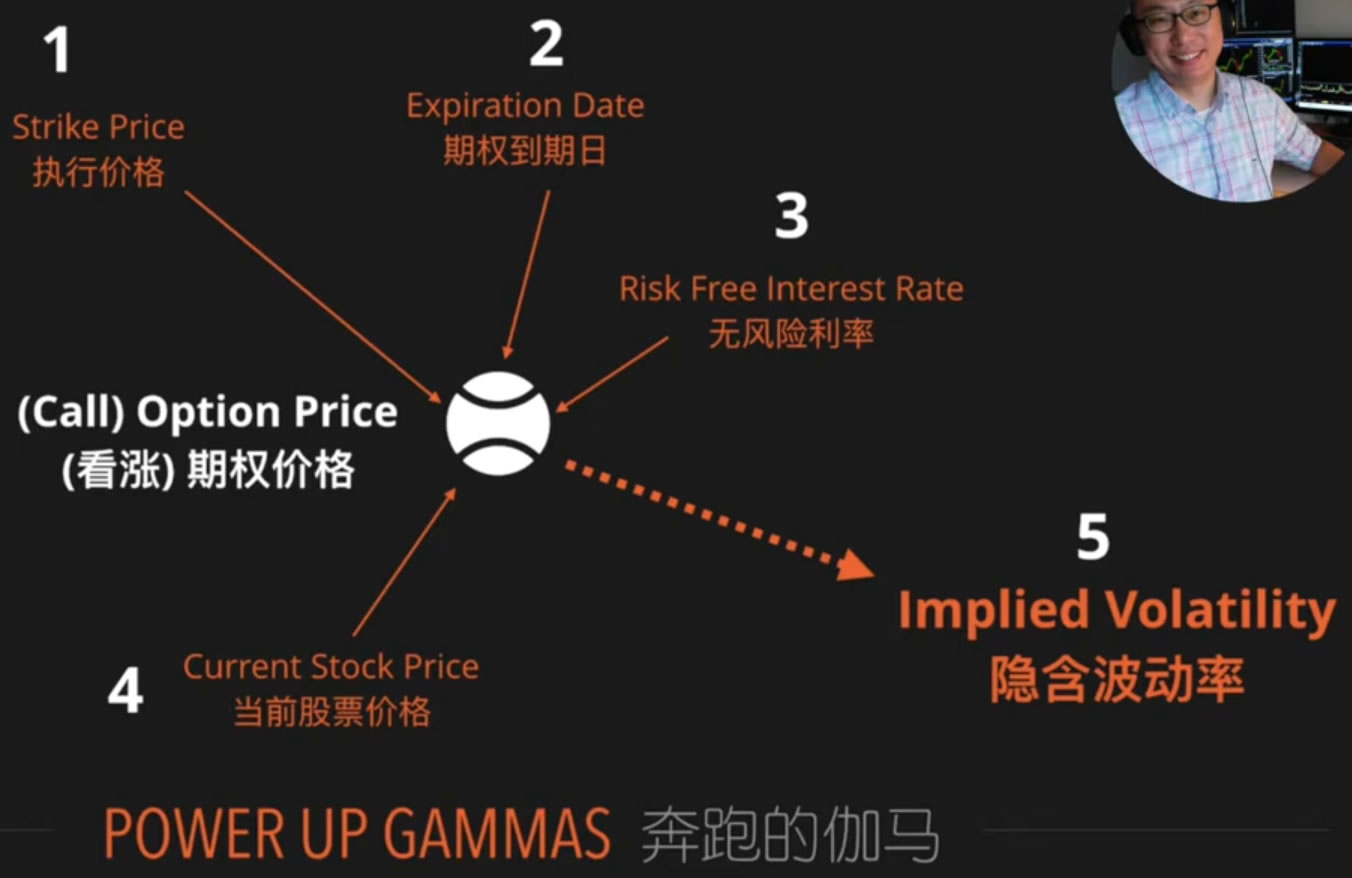
影响期权价格的因素
欧式期权的定价模型:Black-Scholes
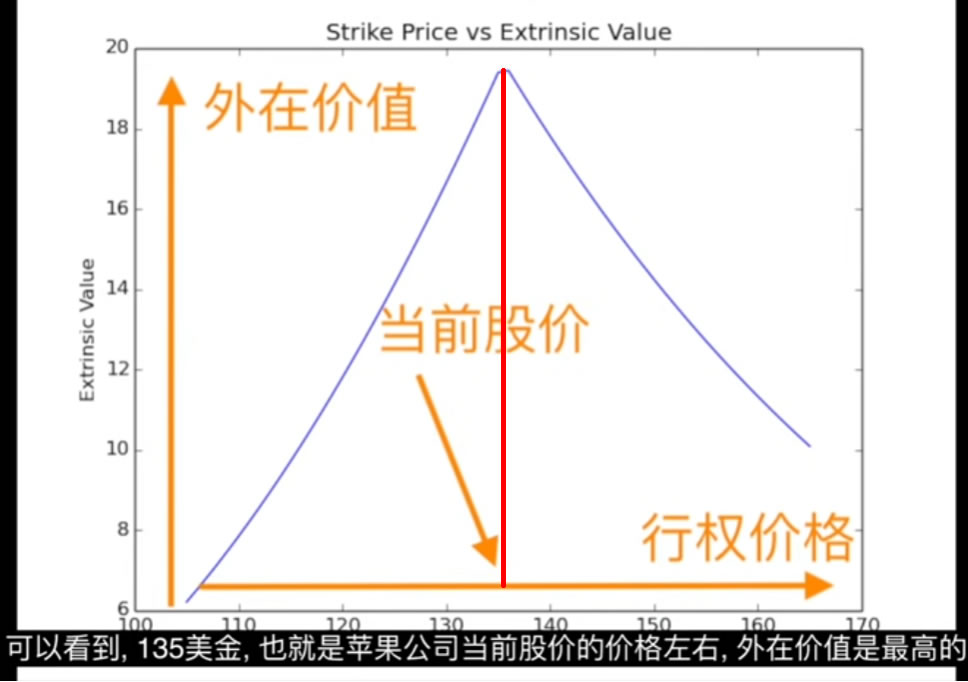
内在价值大约等于0的为平值期权,英文叫ATM(At The money),内在价值>0叫实值期权,英文叫ITM(In The Money),内在价值<0叫虚值期权,英文叫OTM(Out Of Money),就是说虚值期权的价格为0。
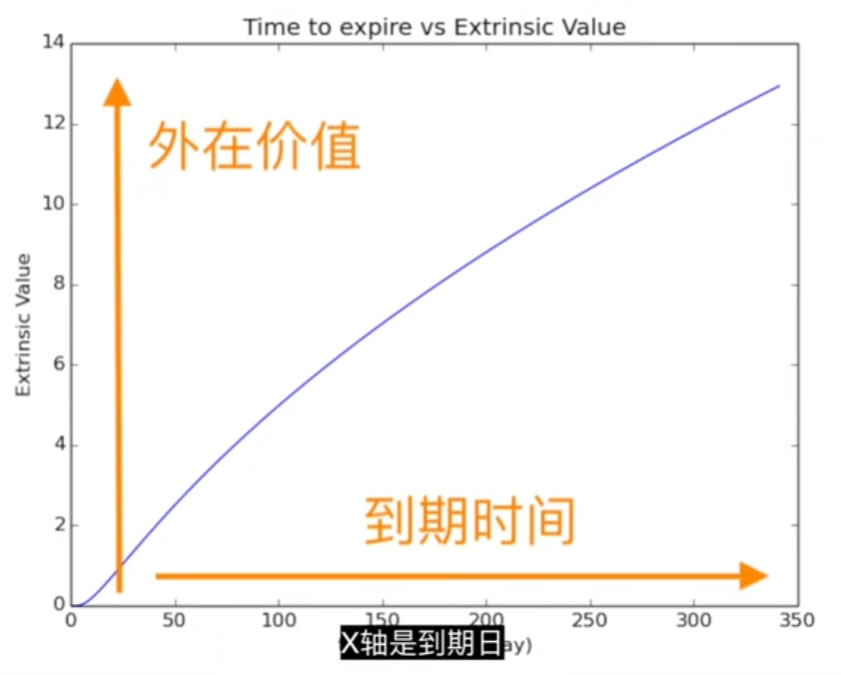
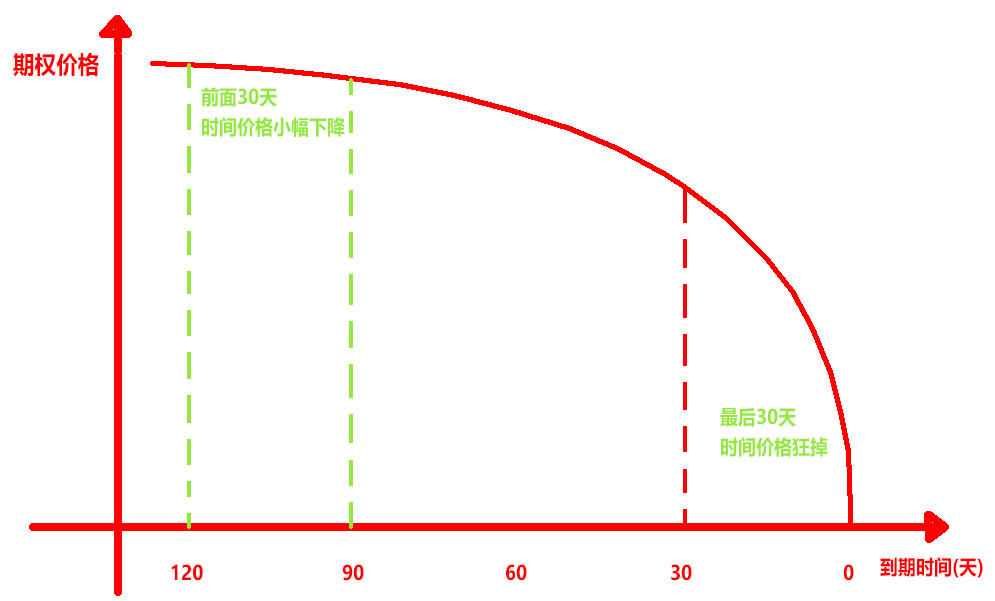
随着期权的到期日一天一天的减少,价值也会一天一天的减少,最后的一段时间每天减少的价值越大。用希腊字母Theta表示,例如Theta为-14,表示期权每天减少14元。
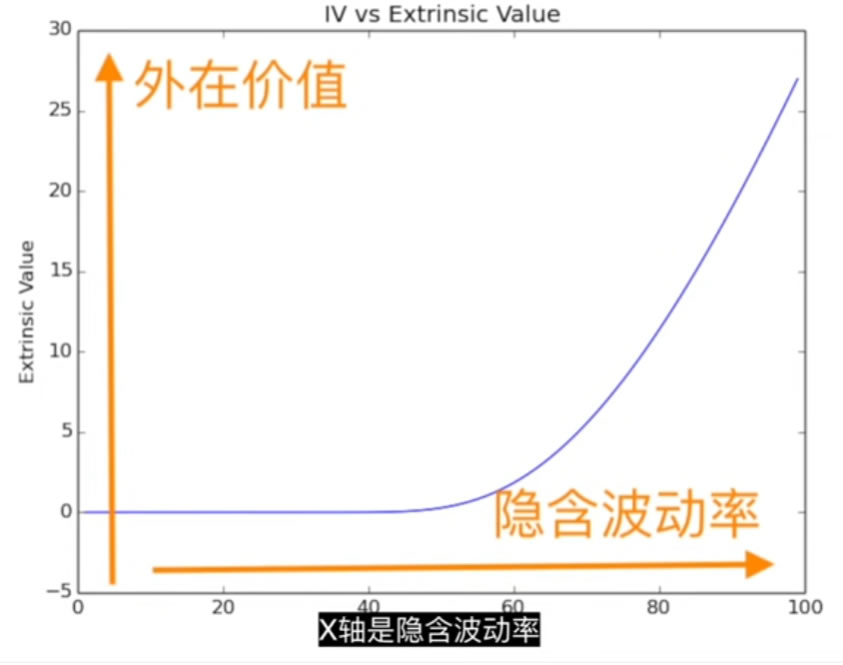
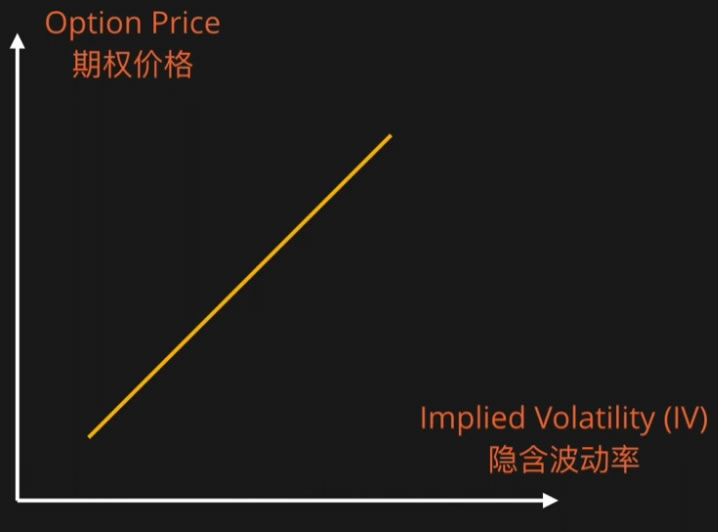
隐含波动率一旦突破某个百分比,期权价值会显著提供,例如上图,一旦IV突破60%左右以上,期权价格显著升高。
隐含波动率最高可以去到500%,然后会下降。
期权的三要素DTV
Delta是期权价格变化的大小。
买入期权时,不要现在Delta小于0.5的期权。
(2)Time 时间 (Theta)-> T
(3)Volatility(Vega)-> V
期权的4个希腊字母
1.Delta
定义:Delta是期权价格移动的快慢。就是说我标的资产价格变化1元,期权价格变化多少?这个多少就是Delta的值。
Deleta的绝对值大于0,小于1。例如:如果Delta=0.9,那么当当标的资产上涨1元,那么期权价格就是上涨0.9元,所以Buy Call Options时,要选择Delta>0.5的来买。可参考视频:https://www.youtube.com/watch?v=Ra7rJlQwEOs&list=PLJ_Kv0UPe7k05J10_fIfpV1sofQyT35WT&index=6
https://www.youtube.com/watch?v=JFJ291ol528
https://www.youtube.com/watch?v=CtoVuv6xvKE
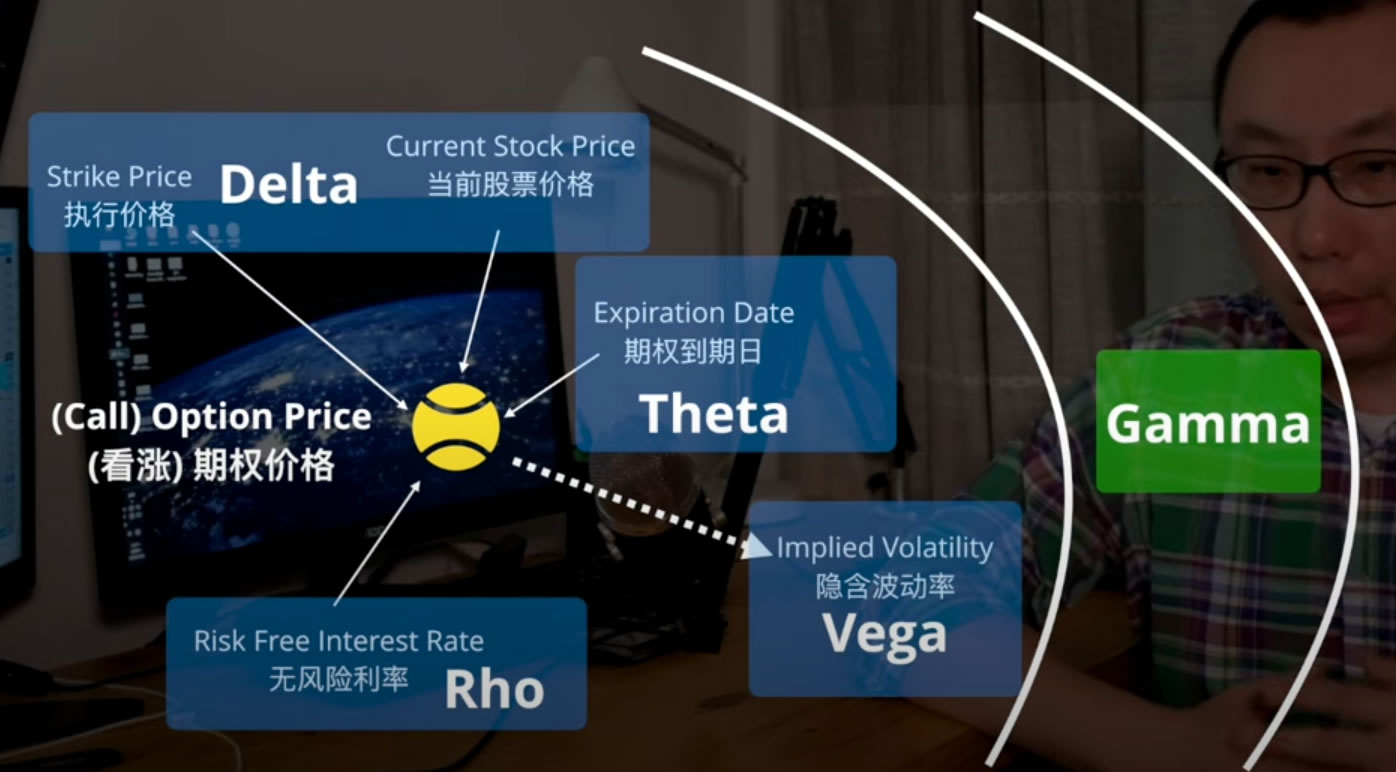
Gamma
我们前面已经讨论过,Delta是期权价格或期权费因标的期货价格变化而造成的变动。
现在,我们将讨论Delta本身是如何跟随标的期货价格变化而变动的,也就是Gamma。请将Gamma看作为Delta的Delta。
换个方式来说,若您驾驶汽车的车速为30 mph(读音:每小时30英里)。要是您提速到40 mph,也就是每小时提速了10英里。如果将速度看成Delta,那么车速的变动便是Gamma。换言之,Gamma就是您的加速度。
期权的策略
一 买入夸式期权
同一行权价、同一行权日买入相同的CALL和PUT期权,配成Delta=0。
作用:只要标的物的价格在短期内发生大的波动,就可以获利。
损益图:
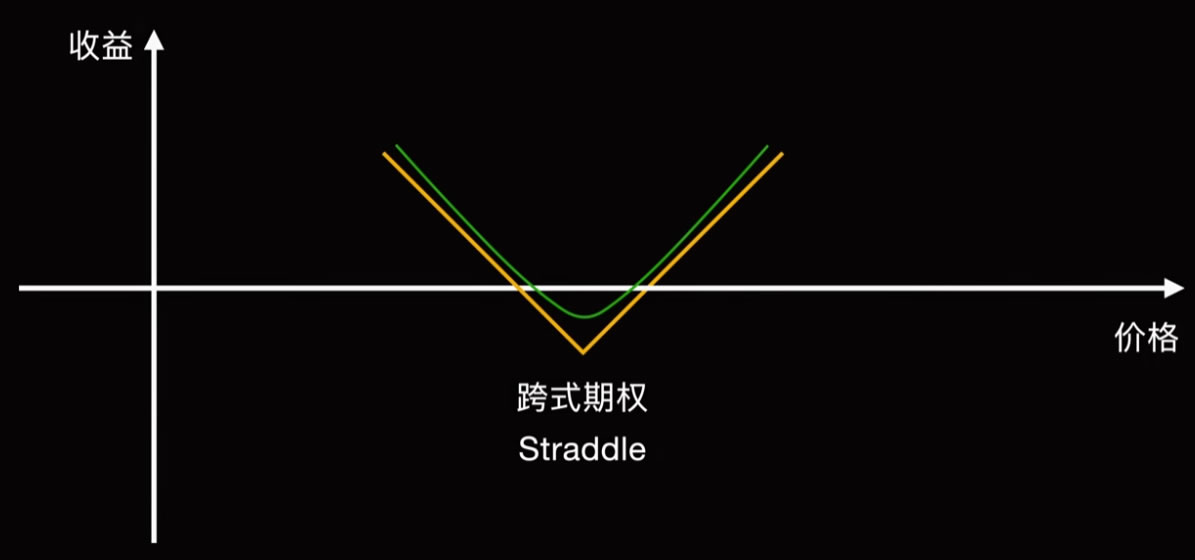
亏损:买入两个期权的价格之和。
收益:理论无限。
应用场景:预期标的物价格短期会发生剧烈波动。例如:年报公布前。
核心:做多波动率Vega。
IV小时买入期权,IV大时卖出期权。IV=隐含波动率。
期权的时间杠杆倍数=标的价格/期权金额*Delta